背景
之前在研究Object Detection的时候,只是知道Precision这个指标,但是mAP(mean Average Precision)具体是如何计算的,暂时还不知道。最近做OD的任务迫在眉睫,所以仔细的研究了一下mAP的计算。其实说实话,mAP的计算,本身有很多现成的代码可供调用了,公式也写的很清楚,但是我认为仔细的研究清楚其中的原理更重要。
AP这个概念,其实主要是在信息检索领域(information retrieval)中的概念,所以这里会比较快速的过一下这个在信息检索领域是如何起作用的。
Precision,Recall,以及Accuracy
Precision和Recall
Precision其实就是在识别出来的图片中,True positives所占的比率:
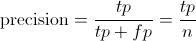 其中的n代表的是(True positives + False positives),也就是系统一共识别出来多少照片 。
其中的n代表的是(True positives + False positives),也就是系统一共识别出来多少照片 。 Recall 是被正确识别出来的个数与测试集中所有的个数的比值:
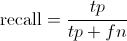 Recall的分母是(True positives + False negatives),这两个值的和,可以理解为一共有多少张飞机的照片。
Recall的分母是(True positives + False negatives),这两个值的和,可以理解为一共有多少张飞机的照片。
如下图所示,假如一个用户向系统提交一个查询(例如“什么是猫”),系统返回了一系列查询的结果,这些结果是系统根据用户提交的信息,判定出来系统内所有跟这个信息有关的结果。
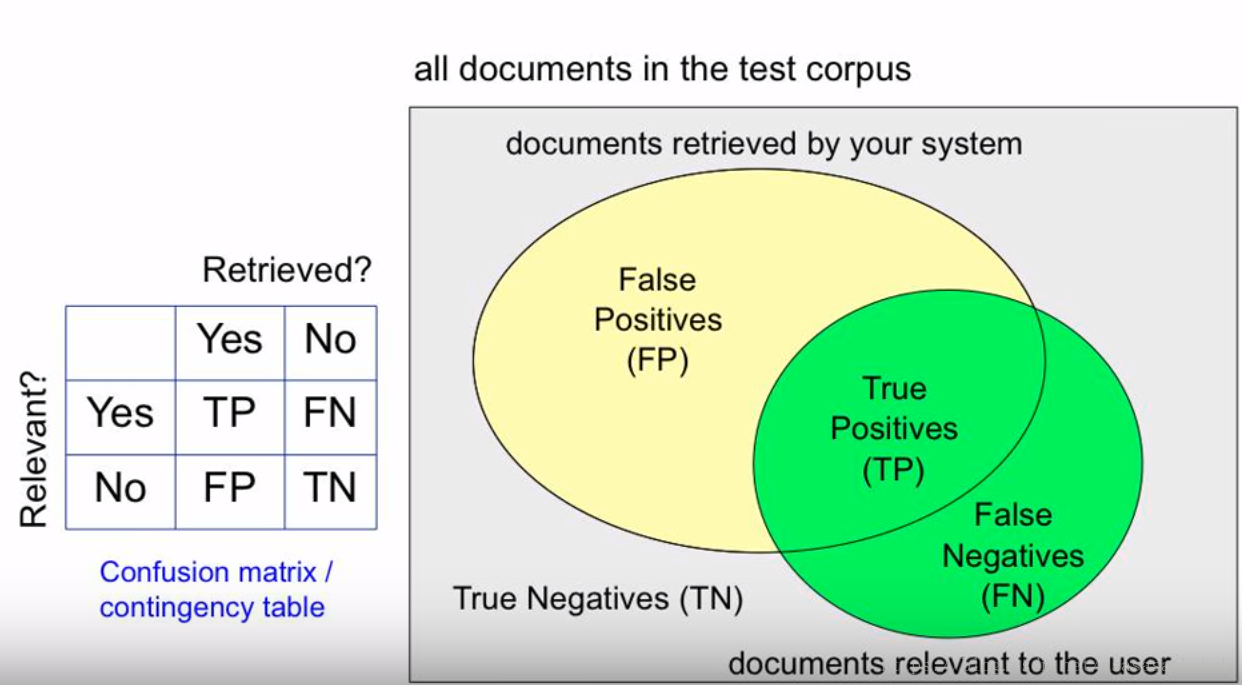
在这个结果里,黄色的部分是系统返回的结果,绿色的部分是总共对用户有用的结果。两者的交集,也就是中间的地方,通常叫做True Positive(TP),中文译名是真阳。而返回结果的剩下的部分,则是False Positive。也就是假阳,意思就是说这些本身是对用户没啥用的,但是系统判定这些对用户有用并且提交给用户了,所以叫“假阳”。而绿色部分剩下的,False Negative,假阴,则是本来对用户有用的结果,但是被系统判定没用,“假阴”。剩下的灰色地方则是True Negative,“真阴”,就是真的没啥用的结果。
Precision是提交给用户的结果里边,究竟有多少是对的,或者反过来说,我们给了用户多少没用的垃圾。Recall是一共有这么多的有用结果,系统究竟能判定出来多少是有用的(能够检出多少?),或者反过来说,我们究竟丢了多少有用的。这两个数是成对出现,单独出现没有意义。为什么这么说?一个例子是我可以轻轻松松将recall提高到100%,那就是不管用户查询啥,我都把系统内所有的文档都给他,这样肯定没丢东西,但是用户也没法得到的好的结果。
为什么不用准确率(accuracy)?
准确率,也就是accuracy,
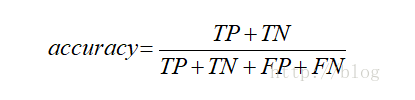
是系统究竟做对了多少。如果是对于平衡样本来说,这个没问题。但是对于样本不平衡的情况,这就不行。例如信息检索,有99.999%的信息都对用户没用,而且大部分系统肯定都能判别出来这些没用,所以对于绝大部分系统,准确率都是99.999%,这个就不能很好的衡量系统性能了。再比如一个90个正样本,10个负样本数据,如果全部分类为正则准确率为90%,这样评价不能客观反映分类器对不平衡数据的性能。
F Score
但是我们还是希望有一个数能够衡量系统的性能,否则系统A的precision比系统B高,但是recall却比系统B低,那么我们就不太好选了。所以综合Precision和Recall,我们得到一个F Score:
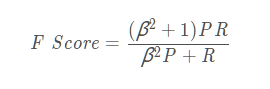
这个F Score是P和R的调和平均数(harmonic mean),β的作用是表明P与R谁比较重要。harmonic mean有个特点,就是假如其中一个P或者R比较小,那么整体就会很小,也就是对两个数中如果有特别小的数的惩罚(penalty)比较大。这是代数平均数所没有的特性。一般来说,会把β设置成1,这个时候就成为F1 Score。几何表达如下图所示。

Precision and Recall Over Ranks
用户提交一个检索Query,得到的结果其实是一个列表,也就是一个有序表,这个表里饱含着所有检索的结果。这个表的序,其实也反映了系统的性能。如果系统把有用的信息排到特别后边,把没用的信息放到前边,也是一个比较性能差的系统。对于一个ranking,我们如何评估它的性能呢?
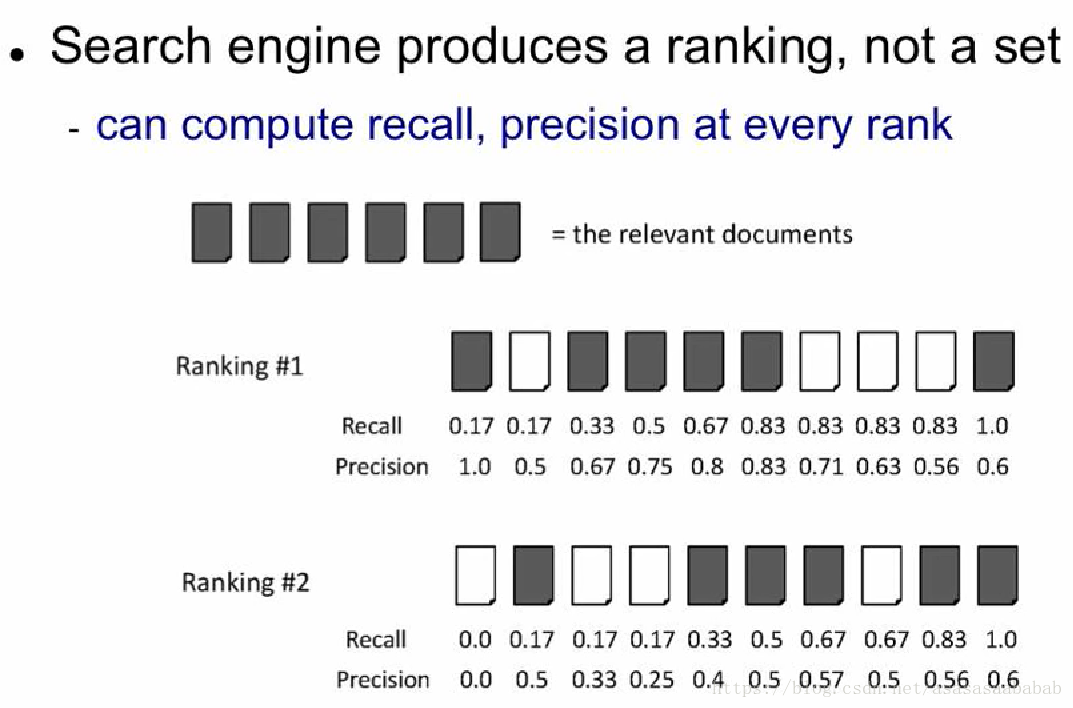
如上图所示,假设对于已经排好序的检测结果:
我们首先在每一个元素上都计算一下precision和recall。计算的方法是:对于第N个元素的precision和recall,计算前N个元素的recall和precision。
举例说明:对于Ranking #1,第一个元素,前1个元素也就是这个元素了,它的recall是1/6=0.17,因为检出了1个,一共有6个需要检出的元素,而precision则是1/1=1,因为一共有1个元素,检出了1个元素,所以是1。
对于Ranking #1 第二个元素的precision和recall,则recall是1/6=0.17。第二个是错的,所以precision是1/2=0.5,因为一共有2个元素。那么对比Ranking #1和#2,我们可以看到因为排序不同,所以precision不一样。这是因为这种计算方法会给靠前的元素比较大的bias。这样precision就可以衡量序在结果中的作用了。
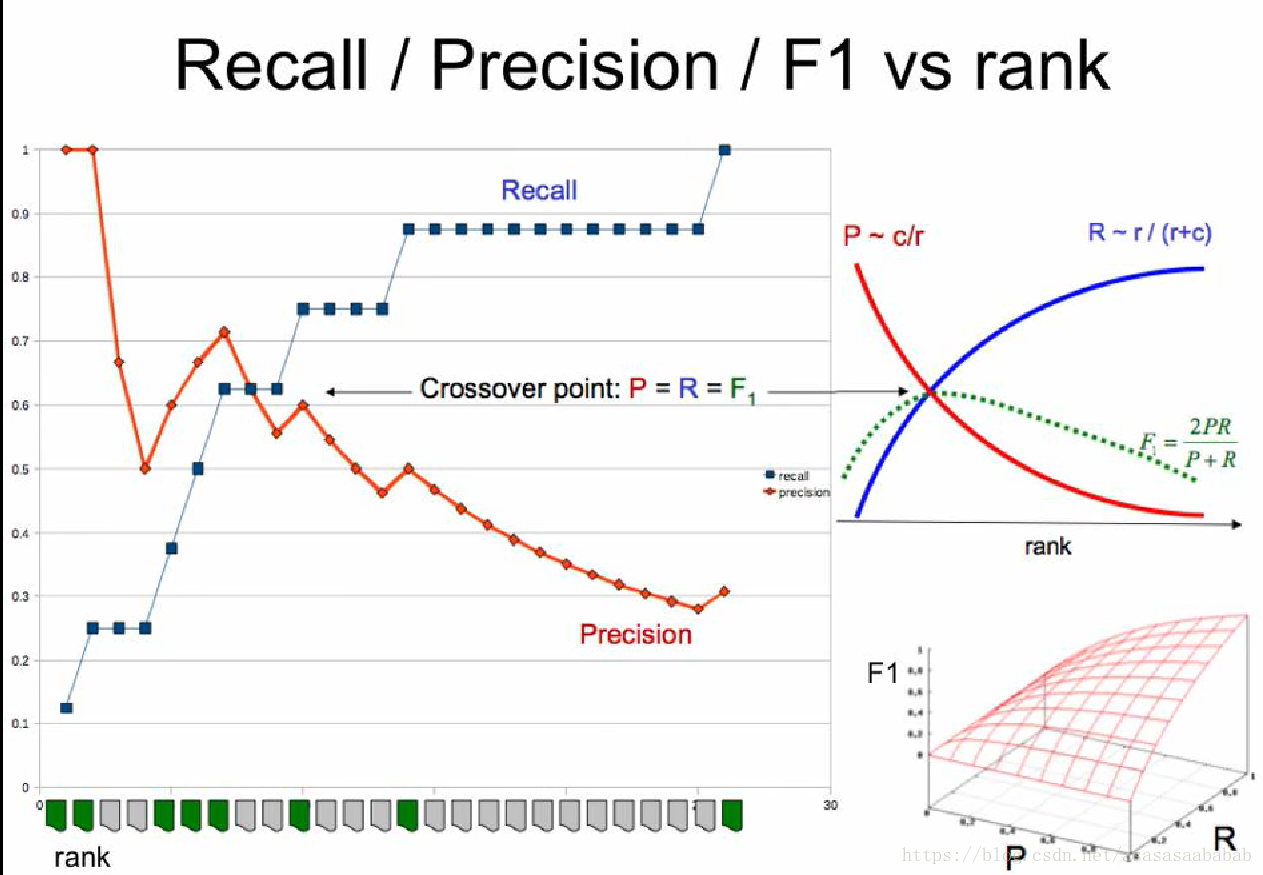
如此我们便可以画出Recall-Precision的关系,以及F1的结果。一般来说,F1 Score会在Recall-Precision相交的地方达到最大值,但是这也不一定。毕竟这个极值其实还是需要满足一定的条件的。但是整体趋势就如同右上的那个小图那样子。
P-R曲线
Interpolated Recall-Precision Plot
我们把上一节计算出来的Recall和Precision画出来,得到如下图所示的结果:
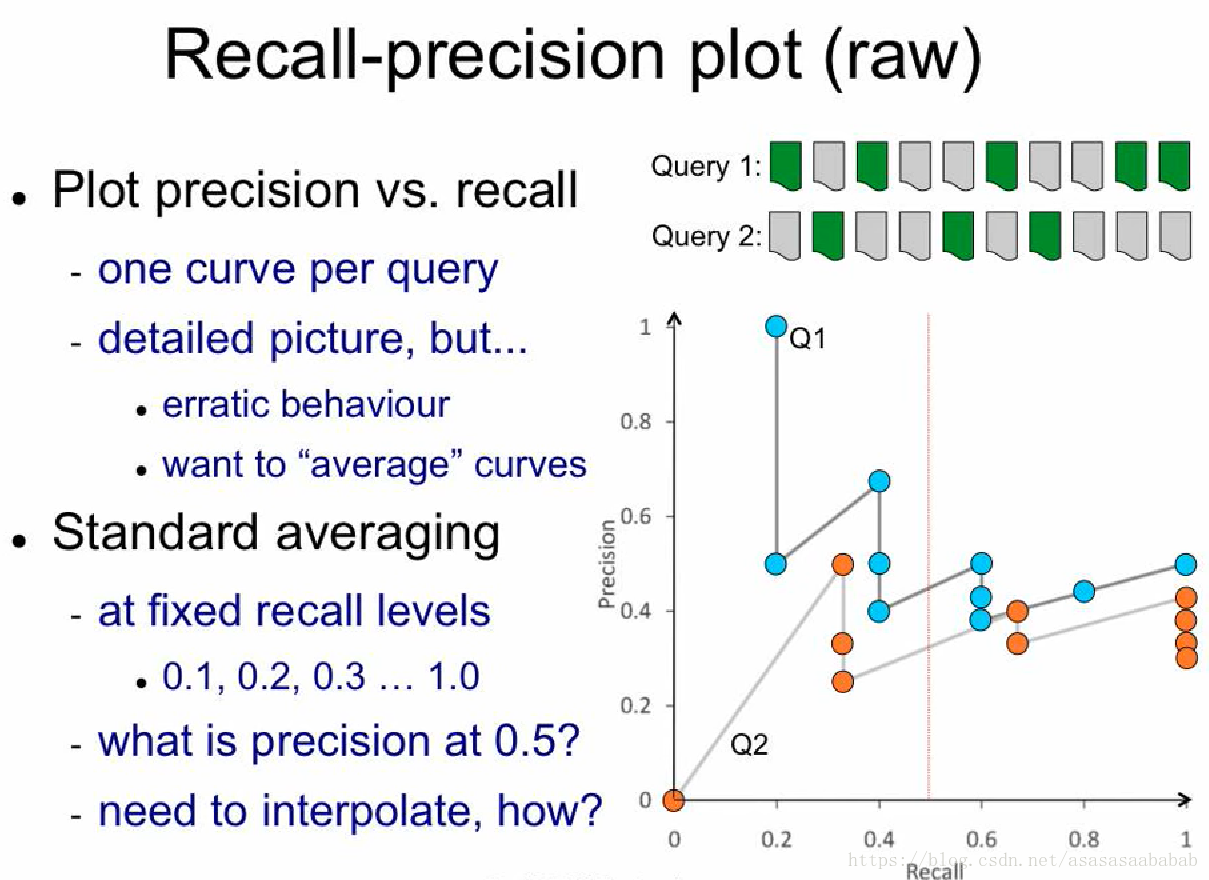
这个曲线就比较蛋疼了。它压根不是一个函数。我们想知道Query 1 Recall = 0.5的情况下,Precision是多少,这事儿完全没法用普通的插值来弄。但是我们知道的是,Precision-Recall的曲线,趋势是下降的,所以前人就提出一种差值方法:任给一个Recall值,它对应的Precision值就等于它最近的右侧的那个“有值”Precision值中最大的那个值。举个例子,例如那个黑色的线,当recall=0.3的时候,它对应的precision值就是0.3右侧最近的有值的,也就是recall=0.4的那个值,但是recall=0.4对应很多值,包括了0.75、0.5和0.4,则选那个最大的0.75,如下图所示:
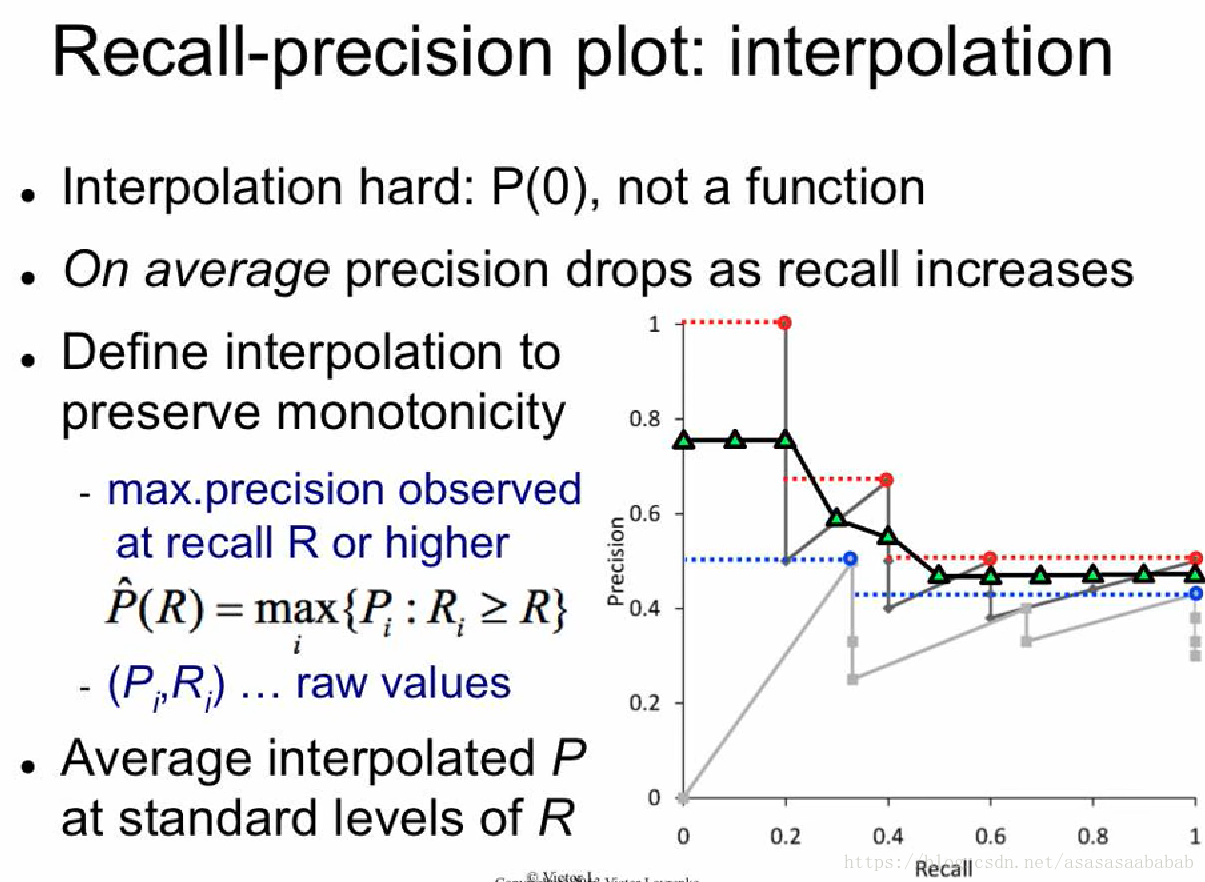
红色的线和蓝色的线就分别是Query 1和2的Interpolated Recall-precision plot。然后对于整体系统,就可以平均一下Q1和Q2的结果,得到一个平均性能。
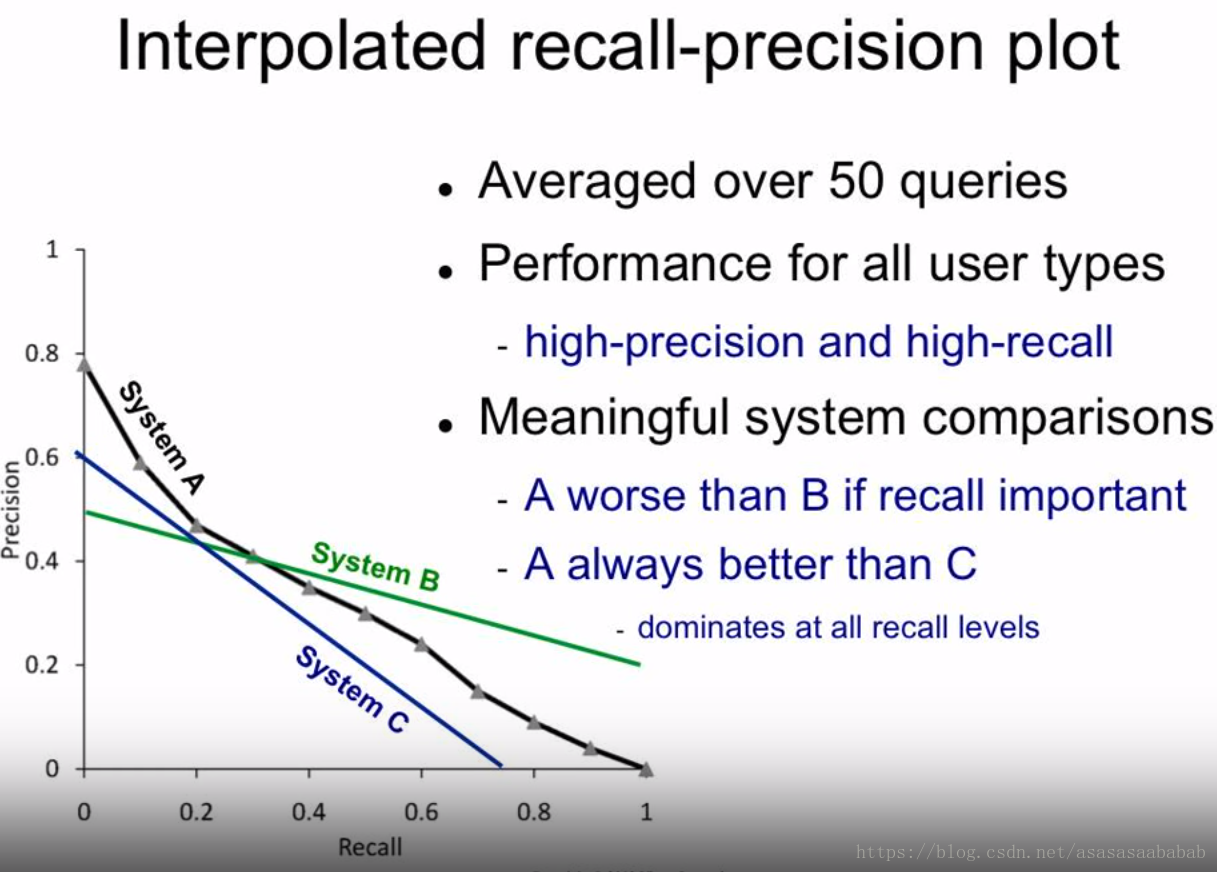
有了这个插值完的曲线,我们就可以对不同系统进行一个性能分析,如上图所示。图中的结论都很简单明了。
Mean Average Precision
到这里,mAP的定义其实就自然而然的明确了。Average Precision,就是对一个Query,计算其命中时的平均Precision,而mean则是在所有Query上去平均,例子如下图所示,一看就明了了。

目标检测中的mAP
回到我们目标检测中的mAP,这个概念是PASCAL VOC比赛中所明确的metric。它的意思是输出的结果是一个ranked list,里边每一个元素包含了类别、框的信息,以及confidence,这个confidence就用来排序。有了排序,就可以计算AP了,然后再针对所有分类,取一个mean,就得到了mAP。这里为何要排序呢?是因为每一个框有一个confidence,mAP作为评估指标,需要考虑confidence进来。比方说我给出一个框,说我有99%的信心这里有一个猫,结果这里没有,相比我给出一个框,说我有10%的信心这里有一个猫,结果也没有,这两个框的penalty和reward不能一样的。因为99%信心说有,结果没有,那就说明这个系统很有问题。反之,假如我给出一个框,99%的信心说有一个猫,然后真有猫,相比10%信心说有猫,结果也是有猫,这两个框也不一样。也就是越“靠谱”,reward越大。什么叫靠谱?靠谱的意思是信心足的时候,一般结果正确。所以我们根据confidence进行排序之后,就应该给排名靠前的结果,也就是confidence比较大的一些更大的权重。所以才会有ranked list。或者可以理解为,我有一个query,查询的内容是,系统中的图片里猫都在那儿?那么这个就肯定需要ranked list了。
值得一提的是在2010年之前,VOC比赛用的AP计算方法并不是上边所述的计算方法,而是对interpolated 的那个图均匀取11个点,[0.0 0.1 0.2 … 1.0]然后求平均。后来才成上边所述的AP计算方法。
贴一段python的ap计算代码放在下边供参考:


def voc_ap(self, rec, prec, use_07_metric=True): if use_07_metric: ap = 0. # 2010年以前按recall等间隔取11个不同点处的精度值做平均(0., 0.1, 0.2, …, 0.9, 1.0) for t in np.arange(0., 1.1, 0.1): if np.sum(rec >= t) == 0: p = 0 else: # 取最大值等价于2010以后先计算包络线的操作,保证precise非减 p = np.max(prec[rec >= t]) ap = ap + p / 11. else: # 2010年以后取所有不同的recall对应的点处的精度值做平均 # first append sentinel values at the end mrec = np.concatenate(([0.], rec, [1.])) mpre = np.concatenate(([0.], prec, [0.])) # 计算包络线,从后往前取最大保证precise非减 for i in range(mpre.size - 1, 0, -1): mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i]) # 找出所有检测结果中recall不同的点 i = np.where(mrec[1:] != mrec[:-1])[0] # and sum (\Delta recall) * prec # 用recall的间隔对精度作加权平均 ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1]) return ap
ROC曲线
(受试者操作特征(Receiver Operating Characteristic),roc曲线上每个点反映着对同一信号刺激的感受性) 对于0,1两类分类问题,一些分类器得到的结果往往不是0,1这样的标签,如神经网络,得到诸如0.5,0,8这样的分类结果。这时,我们人为取一个阈值,比如0.4,那么小于0.4的为0类,大于等于0.4的为1类,可以得到一个分类结果。同样,这个阈值我们可以取0.1,0.2等等。取不同的阈值,得到的最后的分类情况也就不同。 如下面这幅图: 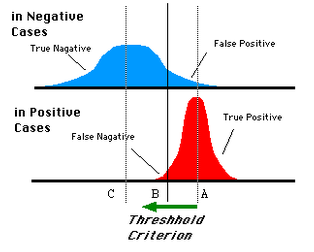 蓝色表示原始为负类分类得到的统计图,红色为正类得到的统计图。那么我们取一条直线,直线左边分为负类,右边分为正,这条直线也就是我们所取的阈值。 阈值不同,可以得到不同的结果,但是由分类器决定的统计图始终是不变的。这时候就需要一个独立于阈值,只与分类器有关的评价指标,来衡量特定分类器的好坏。 还有在类不平衡的情况下,如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%。但这显然是没有意义的。 如上就是ROC曲线的动机。 ROC空间将假正例率(False Positive Rate, 简称FPR)定义为 X轴,真正例率(True Positive Rate, 简称TPR)定义为 Y 轴。这两个值由上面四个值计算得到,公式如下: TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
蓝色表示原始为负类分类得到的统计图,红色为正类得到的统计图。那么我们取一条直线,直线左边分为负类,右边分为正,这条直线也就是我们所取的阈值。 阈值不同,可以得到不同的结果,但是由分类器决定的统计图始终是不变的。这时候就需要一个独立于阈值,只与分类器有关的评价指标,来衡量特定分类器的好坏。 还有在类不平衡的情况下,如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%。但这显然是没有意义的。 如上就是ROC曲线的动机。 ROC空间将假正例率(False Positive Rate, 简称FPR)定义为 X轴,真正例率(True Positive Rate, 简称TPR)定义为 Y 轴。这两个值由上面四个值计算得到,公式如下: TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
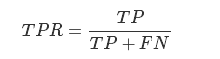
FPR:在所有实际为反例的样本中,被错误地判断为正例之比率。
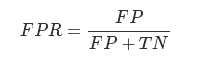
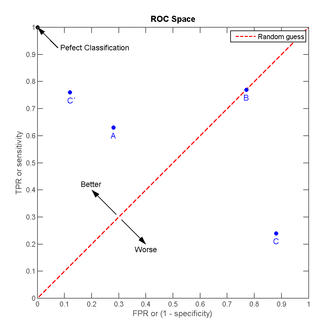 我们可以看出,左上角的点(TPR=1,FPR=0)(TPR=1,FPR=0),为完美分类。曲线距离左上角越近,证明分类器效果越好。点A(TPR>FPR)表明判断大体是正确的。中线上的点B(TPR=FPR)表明判定一半对一半错(这种最垃圾~~);下半平面的点C(TPR<FPR)说明判定大体错误。
我们可以看出,左上角的点(TPR=1,FPR=0)(TPR=1,FPR=0),为完美分类。曲线距离左上角越近,证明分类器效果越好。点A(TPR>FPR)表明判断大体是正确的。中线上的点B(TPR=FPR)表明判定一半对一半错(这种最垃圾~~);下半平面的点C(TPR<FPR)说明判定大体错误。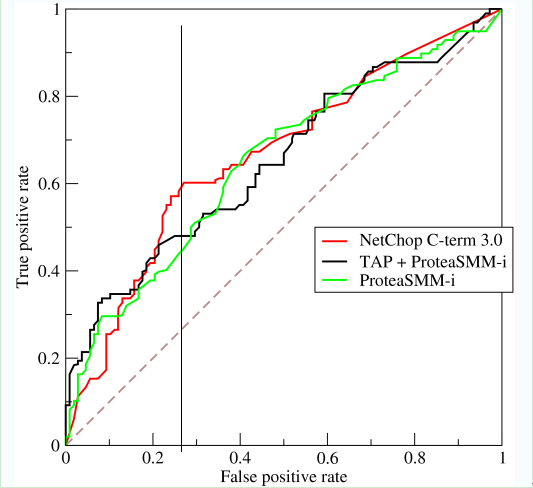 如上,是三条ROC曲线,在0.23处取一条直线。那么,在同样的低FPR=0.23的情况下,红色分类器得到更高的PTR。也就表明,ROC越往上,分类器效果越好。我们用一个标量值AUC来量化它。
如上,是三条ROC曲线,在0.23处取一条直线。那么,在同样的低FPR=0.23的情况下,红色分类器得到更高的PTR。也就表明,ROC越往上,分类器效果越好。我们用一个标量值AUC来量化它。 AUC(Area Under ROC Curve)
auc其实就是ROC曲线围成的面积!!在两个分类器的ROC曲线交叉的情况下,无法判断哪个分类器性能更好,这时可以计算ROC曲线下面积AUC,作为性能度量,面积越大则越好。
为什么使用Roc和Auc评价分类器 既然已经这么多标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变换的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡,即正负样本比例差距较大,而且测试数据中的正负样本也可能随着时间变化。
ROC曲线和Presision-Recall曲线的对比:
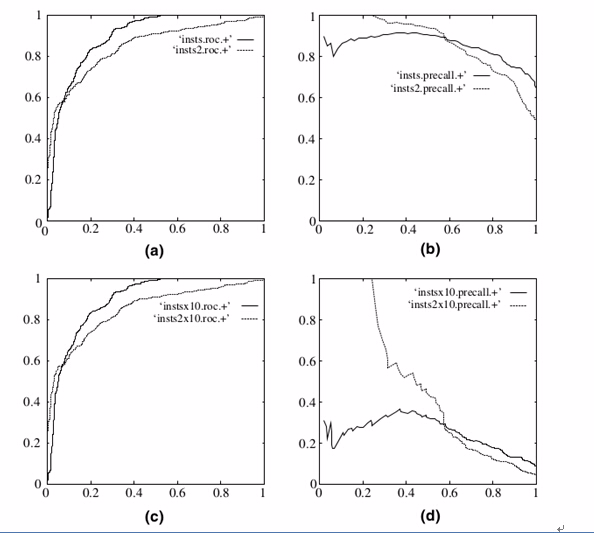 在上图中,(a)和(c)为Roc曲线,(b)和(d)为P-R曲线。
在上图中,(a)和(c)为Roc曲线,(b)和(d)为P-R曲线。 (a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果,可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线变化较大。
以上的Python代码实现大家可以参考这位的博客:
线性回归的决定系数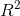 (也称为判定系数,拟合优度)
(也称为判定系数,拟合优度)
相关系数是R哈~~~就是决定系数的开方!
正如题所说决定系数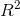 是来衡量回归的好坏,换句话说就是回归拟合的曲线它的拟合优度!也就是得分啦~~
是来衡量回归的好坏,换句话说就是回归拟合的曲线它的拟合优度!也就是得分啦~~
决定系数它是表征回归方程在多大程度上解释了因变量的变化,或者说方程对观测值的拟合程度如何。
计算公式为:

决定系数越大表拟合优度越好!
Python中可直接调用score()方法来计算决定系数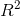 值。
值。
score(self, x_test, y_test, sample_weight=None)
版权声明:本文为转载文章,遵循版权协议,转载请附上原文出处链接和本声明。